1_1 电场与电路
场 作为一个重要的物理概念,最早由英国物理学家法拉第提出。
- 孤立正点电荷的电场。
- 孤立负点电荷的电场。
- 等量同种电荷的电场。
- 等量异种电荷的电场。
- 点电荷与带电平板所形成的电场。
- 匀强电场。
19世纪60年代,麦克斯韦建立了完整的电磁场理论,并预言电磁波的存在。
电、磁都是波,电场在xz平面沿z轴传播。磁场在yz平面沿z轴传播。
电场与电路是紧密联系的概念。电荷在电场的作用下定向移动形成电流,电流所通过的路径则称为电路。
描述电场的物理量如电场强度、电流密度等与描述电路的物理量电压、电流等具有直接的定量关系。事实上电路中的欧姆定律、基尔霍夫定律等可以从麦克斯韦电磁场理论推导得到。
- 电场强度 E
- 磁场强度 H
- 电位移矢量 D
- 磁感应强度 B
- 电流 i
- 电压 u
- 电荷 q
- 磁通量 Φ
利用电荷的有序运动,可以传输能量和信息
当用导线将电源及电子元器件连在一起构成一个导电回路时,电流在金属导线内流动,但电能分布却并非仅在导线之内。(辐射效应。即在导线周围有电能的分布)
当电路的几何尺寸远远小于电路中信号的波长时,电路周围的辐射效应很小,可以忽略不计。这时电流的能量完全分布在金属导线和电路元器件之内,这样的电路称为集总参数电路。这种电路可以用简化的电路模型来描述。
反之,辐射效应明显,电路各处的电流都不一样,电流的能量在空间分布,这样的电路称为分布参数电路。
如:一个音频放大电路工作频率为f=25kHz,则
$$ λ_{波长}=\frac cf=\frac {310^8m/s}{2510^3/s}=12km $$
12km远大于电路尺寸,所以视为集总参数电路
场是路的基础。场是一般问题,路仅是场问题的特殊情况。
- 集总参数电路:可以简化等效电路,用电压、电流等之间的物理量来描述电路。
- 分布参数电路:采用场的观点来分析。
1_2 基本物理变量
电流及电流参考方向
电荷的定向运动形成电流。其大小等于单位时间内通过导体横截面的电荷。数学表达式:
$$ i=\frac {dq}{dt} $$
如:电流从a点到b点每秒有2库伦,则$i=i_{ab}=2A$
如:电流从a点到b点每秒有2库伦,则$i=i_{ba}=-2A$
电压及电压参考方向
电场力将单位正电荷从电场中的a点移到b点所做的功,称为a、 b 两点间的电压。数学表达式:
$$ u=\frac {dw}{dq} $$
习惯上,在电场力的作用下,如果正电荷从A点移动到B点失去电场能量,则A点为正极,B点为负极。
关联参考方向
分析电路时,电压、电流都要事先假定其参考方向。他们之间彼此没有关系,可以任意假定。但为了方便简化分析,规定关联参考方向,即电流的流入端为电压的正极性。
功率
单位时间内某一段电路消耗(或提供)的能量,称为功率,数学表示:
$$ p =\frac {dw}{dt} = \frac {dw}{dq} * \frac {dq}{dt} = u * i $$
电压和电流均为代数量,其乘积功率也是。在关联参考方向的前提下,正功率代表吸收功率,负功率代表发出功率。
例
$ P_{1Ω} = ui = 1W $
$ P_{1V} = ui = -1W $
1_3 基尔霍夫定律
只要是集总参数电路,基尔霍夫电流定律就适用。
| 基尔霍夫电流定律 | 基尔霍夫电压定律 |
|---|---|
| Kirchhoff Current Law | Kirchhoff Voltage Law |
| KCL | KVL |
常用名称

支路
一个二端元件视为一条支路,其电流和电压分别称为支路电流和支路电压。(如图由6支路)
节点
两条以及两条以上支路的连接点称为节点。(如图有4节点。d、e为一个)
- 广义节点:将电路中的一部分围成一个封闭平面(高斯面),此封闭平面为广义节点。
回路
由支路所组成的闭合路径。(如图有6回路)
网孔
内部不含有支路的回路。(网孔是特殊的一种回路)(如图为3)
KCL
概念
对于集总参数电路中的任一结点,在任一时刻流出该结点的电流代数和等于零。
$$ \sum_{k=1}^{n_{支路数目}} i_k = 0 $$
物理意义
在任一单位时刻流出结点的电荷总数$\frac {dq}{dt} = -i_1 + i_2 - i_3 + i_4 - i_5 = 0$
结点只是理想导体的汇合点,不可能积累电荷,也不可能创造或消灭,根据电荷守恒,必须为零。
总结
- KCL方程是线性齐次代数方程,它表明了各个支路电流所受的线性约束。
- KCL适用于任何集总参数电路。它仅与元件的相互连接方式有关,而与元件的性质无关。所以说,KCL及映了电路的近连性质。
- KCL对集总参数电路中任一假设的闭合面也是适用的。
KVL
与KCL是对偶的
概念
对于集总参数电路中的任一回路,在任一时刻,沿闭合回路绕行一周,各支路电压的代数和等于零
$$ \sum_{k=1}^{n_{支路数目}} u_k = 0 $$
物理意义
电荷沿着回路绕行一周,回到原点,其电势能不变。KVL是电路中能量守恒的体现。
总结
- KVL方程是线性齐次代数方程,它表明了各个支路电压所受的线性约束。
- KVL适用于任何集总参数电路。它仅与元件的相互连接方式有关,而与元件的性质无关。
2_1 电阻元件
定义
如果一个二端元件在任一时刻的电压u与其电流i之间的关系,由 u-i平面上一条曲线确定,则此二端元件称为二端电阻元件,其数学表达式为:
$$ f(u,i)=0 $$
- 特性曲线为通过坐标原点的直线,称为线性电阻,否则称为非线性电阻
- 特性曲线随时间变化的电阻,称为时变电阻,否则成为不变电阻或定常电阻
线性非时变电阻
电阻参数:$ R = \frac ui Ω$
电导参数:$ G = \frac iu S$ (电阻的倒数。单位西门子,简称西)
功率
$$ p = ui = Ri^2 = \frac {ui^2}{R} = Gu^2 = \frac {i^2}{G} $$
- 负电阻可以发出功率,也称有源电阻
2_2 独立电源
实际电源的两个理想化
- 可以对外提供无穷大的能量
- 输出的电压或电流不随外接电路变化
- 独立电压源
- 独立电流源
定义
电压源:如果一个二端元件的电流无论为何值,其电压保持常量$U_s$或按给定的时间函数$u_s(t)$变化,则此二端元件称为独立电压源,简称为电压源。
其功率:在关联参考方向下,电压源的吸收功率为:$P_s = U_sI_s$。其值可正可负可零。
电流源:如果一个二端元件的电压无论为何值,其电流保持常量$I_s$或按给定的时间函数$i_s(t)$变化,则此二端元件称为独立电流源,简称为电流源。
其功率:关联参考方向下,电流源的吸收功率为:$P_s = I_sU_s$。其值可正可负可零
2_3 两类约束与2b方程
电路的总体特性包含:元件特性与连接特性(拓扑特性)
元件约束:由元件的VCR(电压电流关系)描述。VCR反映了电路元件对所在支路的电压、电流之间所起的一种约束关系。
拓扑约束:基尔霍夫定律KCL、KVL描述对支路的电压、电流约束。
应用两类约束建立的电路方程称为2b方程。
2b方程
2b方程是指以b个支路电流和b个支路电压作为变量建立的一组数目为2b的方程组
对于具有b条支路n个节点的平面连通电路,可以列出线性无关的方程为:
$$ \begin{cases}
(n-1)个KCL方程\
(b-n+1)个KVL方程\
b个二端元件的VCR方程\
\end{cases} $$
2b方程式求解电路最基本的电路方程,分析电路的基本依据
2_4 支路电流法与支路电压法
对于仅由独立电压源和线性二段电阻构成的电路,可将欧姆定律$u=Ri$代入KVL方程中,消去全部电阻支路电压,变成以直流电流为变量的KVL方程。加上原来的KCL方程,得到以b个支路电流为变量的b个线性无关的方程组,称为支路电流法方程。
(简而言之,将欧姆定律代入消元)
在2b方程的基础上,我们将电阻元件的VCR方程 $i= Gu$ 带入到KCL方程中,将支路电流转换为支路电压,得到$n-1$个支路电压作为变量的KCL方程,加上原来的$b-n+1$个KVL方程,得到以b个支路电压为变量的b个线性无关的方程组,称为支路电压法方程。
(简而言之,将$i=Gu$代入消元)
3_1 线性无源单口的等效
线性电阻的串联
$$
u = u_1 + u_2 + … + u_n = R_1i_1 + R_2i_2 + … + R_ni_n = (R_1 + R_2 + … + R_n)i\
$$
线性电阻的并联
(G是电阻的倒数)
$$
i = i_1 + i_2 + … + i_n = G_1u_1 + G_2u_2 + … + G_nu_n = (G_1 + G_2 + … + G_n)u\
$$

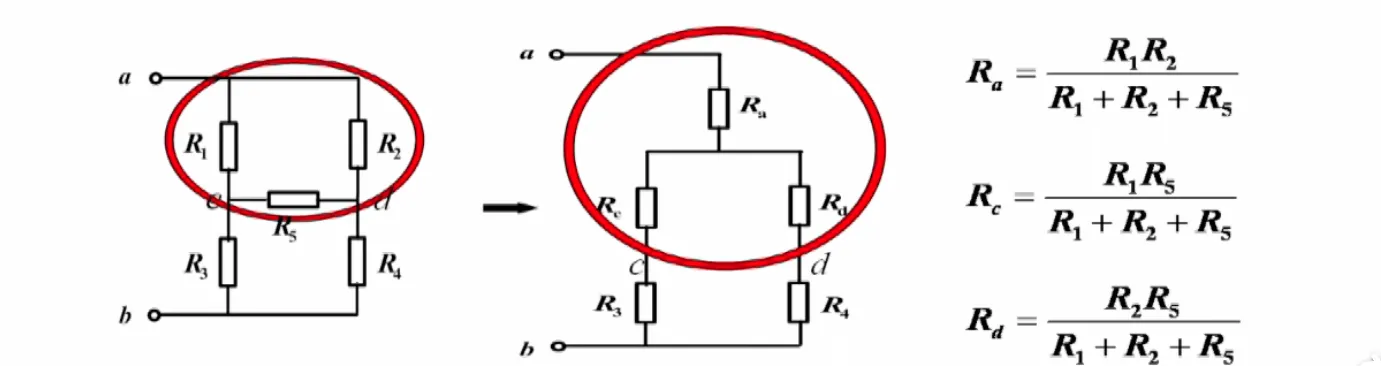
电阻三角形联结等效变换为电阻星型联结的公式为
$$R_i = \frac {接于i端两电阻乘积}{△连接三电阻之和}$$